sábado, 2 de junio de 2012
jueves, 24 de mayo de 2012
La habitación de Fermat (Enigmas)
- Enigma 1:
¿Qué patrón sigue la siguiente secuencia de números:
5 – 4 – 2 – 9 – 8 – 6 – 7 – 3 – 1?
Solución 1: Los números están ordenados alfabéticamente:
cinco – cuatro – dos – nueve – ocho – seis – siete – tres – uno.
- Enigma 2:
Un pastelero recibe tres cajas opacas. Una caja contiene caramelos de menta, otra caramelos de anís y otra un surtido de caramelos de menta y anís. Las cajas tienen etiquetas que ponen caramelos de menta, anís o mezclados. Pero el pastelero recibe el aviso de que todas las cajas están mal etiquetadas, ¿Cuántos caramelos tendrá que sacar el pastelero como mínimo para verificar el contenido de las cajas?
Solución: 1 caramelo.
Ya que si se saca uno de la caja donde dice “mezclados”, se podrá identificar el tipo de caramelo que contiene la caja, si el caramelo que se saco es de anís, entonces en la caja donde están los caramelos de anís estarán los que en verdad son mezclados y en el de “menta” estarán los de anís. Finalmente, será necesario solo un caramelo.
- Enigma 3:
¿Qué código oculto hay detrás de la siguiente lista con 169 dígitos que son únicamente unos o ceros?
- Enigma 4:
En el interior de una habitación herméticamente cerrada, hay una bombilla, y fuera de la habitación, hay tres interruptores. Solo uno de los tres enciende la bombilla, mientras la puerta este cerrada, puedes pulsar los interruptores las veces que quieras. Pero al abrir la puerta, hay que decir cual de los tres interruptores enciende la bombilla.
Solución: Según la temperatura de la bombilla.
Encendemos el primer interruptor y lo dejamos por un momento, luego lo apagamos. Una vez hecho esto encendemos el segundo y abrimos la puerta, si la luz esta prendida entonces el interruptor correcto es el segundo, si la bombilla esta caliente entonces corresponde al primer interruptor.
- Enigma 5:
¿Cómo se pueden cronometrar 9 minutos con 2 relojes de arena de 4 y 7 minutos, respectivamente?.
Solución: Se ponen en marcha los dos relojes a la vez. Cuando el de 4' se acaba al de 7' le quedan 3'. Continúa funcionando el reloj de 7'. Se pone en funcionamiento el reloj de 4'. Cuando el de 7' se acaba al de 4' le queda 1'. Continúa funcionando el reloj de 4'. Se pone en funcionamiento el reloj de 7'. Cuando el de 4' se acaba al de 7' le quedan 6'. Se da la vuelta al reloj de 7' al que ahora le quedaría 1'.
- Enigma 6:
Un alumno pregunta a un profesor por las edades de sus tres hijas:
P – El producto de las edades es 36 y si las sumas coincide con el número de puerta de tu casa.
A – De acuerdo, pero necesito otro dato más.
P – Es cierto. La mayor toca el piano.
¿Qué edad tienen las hijas del profesor?
Solución: En principio sabemos que el número 36 es el producto de tres factores (la edad de las tres hijas).
Descomponiendo dicho producto se obtienen las siguientes fórmulas o planteamientos:
1 x 1 x 36 = 36
1 x 2 x 18 = 36
1 x 3 x 12 = 36
1 x 4 x 9 = 36
1 x 6 x 6 = 36
2 x 2 x 9 = 36
2 x 3 x 6 = 36
3 x 3 x 4 = 36
Si todas las sumas de estas fórmulas fueran distintas, el problema pronto quedaría resuelto, pues la suma que coincidiera con el número de la casa donde vive el profesor automáticamente delataría la edad de cada una de las tres hijas. Si hacemos la comprobación, observaremos que todas las ternas suman distinto excepto: 1 + 6 + 6 y 2 + 2 + 9, que ambas suman 13.
De ahí se deduce que el profesor vive en la casa que lleva el número 13, y al tener estas dos posibilidades, el profesor indicó que le faltaba un dato. La aclaración "la mayor toca el piano" descarta la posibilidad de la fórmula 1 + 6 + 6, pues no hay una mayor. Luego las edades son 2, 2 y 9 años.
- Enigma 7: En la Tierra Falsa todos los habitantes mienten siempre, mientras que en la Tierra Cierta todos los
habitantes dicen siempre la verdad. Un extranjero está atrapado en una habitación con dos puertas, una de ellas es la de la Libertad, custodiadas cada una por un vigilante de cada una de las dos tierras. Para abrirla, el extranjero sólo puede hacer una única pregunta a uno de los vigilantes. ¿Qué pregunta debería hacer?
Solución: La pregunta que debo hacer es: "¿Qué me contestaría el otro guardián si le preguntase qué puerta NO me conduce a la libertad?
- Enigma 8: Una madre es 21 años mayor que su hijo. Al cabo de 6 años la edad de la madre será cinco veces la que tenga el hijo. ¿Qué está haciendo el padre?
Solución: Si x es la edad del hijo la de la madre es (21 + x)
La ecuación que tendremos que resolver es: 5 · (x + 6) = (21+x) + 6
La solución es x = -3/4 años
Aparentemente absurdo pero si -3/4 años lo pasamos a meses nos da que x = - 9 meses
¿Qué hace el padre?
¿Qué patrón sigue la siguiente secuencia de números:
5 – 4 – 2 – 9 – 8 – 6 – 7 – 3 – 1?
Solución 1: Los números están ordenados alfabéticamente:
cinco – cuatro – dos – nueve – ocho – seis – siete – tres – uno.
- Enigma 2:
Un pastelero recibe tres cajas opacas. Una caja contiene caramelos de menta, otra caramelos de anís y otra un surtido de caramelos de menta y anís. Las cajas tienen etiquetas que ponen caramelos de menta, anís o mezclados. Pero el pastelero recibe el aviso de que todas las cajas están mal etiquetadas, ¿Cuántos caramelos tendrá que sacar el pastelero como mínimo para verificar el contenido de las cajas?
Solución: 1 caramelo.
Ya que si se saca uno de la caja donde dice “mezclados”, se podrá identificar el tipo de caramelo que contiene la caja, si el caramelo que se saco es de anís, entonces en la caja donde están los caramelos de anís estarán los que en verdad son mezclados y en el de “menta” estarán los de anís. Finalmente, será necesario solo un caramelo.
- Enigma 3:
¿Qué código oculto hay detrás de la siguiente lista con 169 dígitos que son únicamente unos o ceros?
- Enigma 4:
En el interior de una habitación herméticamente cerrada, hay una bombilla, y fuera de la habitación, hay tres interruptores. Solo uno de los tres enciende la bombilla, mientras la puerta este cerrada, puedes pulsar los interruptores las veces que quieras. Pero al abrir la puerta, hay que decir cual de los tres interruptores enciende la bombilla.
Solución: Según la temperatura de la bombilla.
Encendemos el primer interruptor y lo dejamos por un momento, luego lo apagamos. Una vez hecho esto encendemos el segundo y abrimos la puerta, si la luz esta prendida entonces el interruptor correcto es el segundo, si la bombilla esta caliente entonces corresponde al primer interruptor.
- Enigma 5:
¿Cómo se pueden cronometrar 9 minutos con 2 relojes de arena de 4 y 7 minutos, respectivamente?.
Solución: Se ponen en marcha los dos relojes a la vez. Cuando el de 4' se acaba al de 7' le quedan 3'. Continúa funcionando el reloj de 7'. Se pone en funcionamiento el reloj de 4'. Cuando el de 7' se acaba al de 4' le queda 1'. Continúa funcionando el reloj de 4'. Se pone en funcionamiento el reloj de 7'. Cuando el de 4' se acaba al de 7' le quedan 6'. Se da la vuelta al reloj de 7' al que ahora le quedaría 1'.
- Enigma 6:
Un alumno pregunta a un profesor por las edades de sus tres hijas:
P – El producto de las edades es 36 y si las sumas coincide con el número de puerta de tu casa.
A – De acuerdo, pero necesito otro dato más.
P – Es cierto. La mayor toca el piano.
¿Qué edad tienen las hijas del profesor?
Solución: En principio sabemos que el número 36 es el producto de tres factores (la edad de las tres hijas).
Descomponiendo dicho producto se obtienen las siguientes fórmulas o planteamientos:
1 x 1 x 36 = 36
1 x 2 x 18 = 36
1 x 3 x 12 = 36
1 x 4 x 9 = 36
1 x 6 x 6 = 36
2 x 2 x 9 = 36
2 x 3 x 6 = 36
3 x 3 x 4 = 36
Si todas las sumas de estas fórmulas fueran distintas, el problema pronto quedaría resuelto, pues la suma que coincidiera con el número de la casa donde vive el profesor automáticamente delataría la edad de cada una de las tres hijas. Si hacemos la comprobación, observaremos que todas las ternas suman distinto excepto: 1 + 6 + 6 y 2 + 2 + 9, que ambas suman 13.
De ahí se deduce que el profesor vive en la casa que lleva el número 13, y al tener estas dos posibilidades, el profesor indicó que le faltaba un dato. La aclaración "la mayor toca el piano" descarta la posibilidad de la fórmula 1 + 6 + 6, pues no hay una mayor. Luego las edades son 2, 2 y 9 años.
- Enigma 7: En la Tierra Falsa todos los habitantes mienten siempre, mientras que en la Tierra Cierta todos los
habitantes dicen siempre la verdad. Un extranjero está atrapado en una habitación con dos puertas, una de ellas es la de la Libertad, custodiadas cada una por un vigilante de cada una de las dos tierras. Para abrirla, el extranjero sólo puede hacer una única pregunta a uno de los vigilantes. ¿Qué pregunta debería hacer?
Solución: La pregunta que debo hacer es: "¿Qué me contestaría el otro guardián si le preguntase qué puerta NO me conduce a la libertad?
- Enigma 8: Una madre es 21 años mayor que su hijo. Al cabo de 6 años la edad de la madre será cinco veces la que tenga el hijo. ¿Qué está haciendo el padre?
Solución: Si x es la edad del hijo la de la madre es (21 + x)
La ecuación que tendremos que resolver es: 5 · (x + 6) = (21+x) + 6
La solución es x = -3/4 años
Aparentemente absurdo pero si -3/4 años lo pasamos a meses nos da que x = - 9 meses
¿Qué hace el padre?
lunes, 21 de mayo de 2012
La habitación de Fermat
Año: 2007
Duración: 87 minutos
Director: Luis Piedrahita, Rodrigo Sopeña
Guión: Luis Piedrahita, Rodrigo Sopeña
Género: Intriga, Thriller, Thriller psicológico
Fotografía: Miguel Ángel Amoedo
Música: Federico Jusid
Reparto:
-Alejo Sauras (Galois)
-Elena Ballesteros (Oliva)
-Santi Millán (Pascal)
-Lluís Homar (Hilbert)
-Federico Luppi (Fermat)
-Helena Carrión, (Bibliotecaria)
Sinopsis: Cuatro matemáticos, que no se conocen entre sí, son invitados por un misterioso anfitrión con el pretexto de resolver un gran enigma. Pero descubren que la sala en la que se encuentran resulta ser un cuarto menguante... que les aplastará si no descubren a tiempo qué les une y por qué alguien quiere asesinarles
Trailer:
jueves, 10 de mayo de 2012
miércoles, 28 de marzo de 2012
martes, 27 de marzo de 2012
lunes, 26 de marzo de 2012
martes, 20 de marzo de 2012
martes, 24 de enero de 2012
Pelicula Enigma
Duración: 117 minutos
Director: Michael Apted
Guión: Tom Stoppard (Novela: Robert Harris)
Género: Romántica / Thriller / Suspense
Fotografía: Seamus McGarvey
Música: John Barry, Mick Jagger
Reparto:
-Dougray Scott - Tom Jericho
-Kate Winslet - Hester Wallace
-Saffron Burrows - Claire Romilly
-Jeremy Northam - Mr. Wigram
-Nikolaj Coster Waldau - Jozef 'Puck' Pukowski
-Tom Hollander - Logie
-Donald Sumpter - Leveret
-Matthew Macfadyen - Cave
-Corin Redgrave - Admiral Trowbridge
-Nicholas Rowe - Villiers
-Edward Hardwicke - Heaviside
Sinopsis: Segunda Guerra Mundial. Inglaterra, 1943. Los descifradores de códigos de Betchley Park, la estación X, sede de los servicios secretos británicos, se enfrentan a su peor pesadilla: inesperadamente, los submarinos nazis han cambiado el código que utilizan para comunicarse entre sí y con el alto mando alemán. Un convoy de barcos de mercancías aliado que está cruzando el atlántico con diez mil pasajeros e importantes suministros está en peligro de ataque. Las autoridades recurren a Tom Jericho -Dougray Scott-, un brillante matemático y experto descifrador de códigos de la inteligencia británica, el hombre que había conseguido descifrar el anterior código nazi, denominado Enigma, empleado para la flota submarina alemana. Lo que sus colegas no saben es que Jericho tiene un enigma personal que resolver: Claire -Saffron Burrows-, la mujer de la que se ha enamorado desaparece cuando las autoridades empiezan a sospechar que puede haber un espía en Bletchley Park. Para llegar a fondo de ambos misterios, Jericho solicitará la ayuda de Hester -Kate Winslet-, la mejor amiga de Claire.
Tráiler:
lunes, 23 de enero de 2012
Conjetura de Goldbach
En teoría de números, la conjetura de Goldbach es uno de los problemas abiertos más antiguos en matemáticas. A veces se le califica del problema más difícil en la historia Su enunciado es el siguente
"Todo número par mayor que 2 puede escribirse como suma de dos números primos."
Ejemplo:
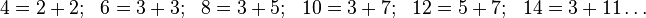
Historia
Esta conjetura había sido conocida por Descartes[cita requerida]. La siguiente afirmación es equivalente a la anterior y es la que se conjeturó originalmente en una carta de Goldbach a Euler en 1742:
Todo número entero mayor que 5 se puede escribir como suma de tres números primos.
Esta conjetura ha sido investigada por muchos teóricos de números y ha sido comprobada por ordenadores para todos los números pares menores que 1018. La mayor parte de los matemáticos cree que la conjetura es cierta, y se basan mayoritariamente en las consideraciones estadísticas sobre la distribución probabilística de los números primos en el conjunto de los números naturales: cuanto mayor sea el número entero par, se hace más "probable" que pueda ser escrito como suma de dos números primos.
Enlace.
"Todo número par mayor que 2 puede escribirse como suma de dos números primos."
Ejemplo:
Historia
Esta conjetura había sido conocida por Descartes[cita requerida]. La siguiente afirmación es equivalente a la anterior y es la que se conjeturó originalmente en una carta de Goldbach a Euler en 1742:
Todo número entero mayor que 5 se puede escribir como suma de tres números primos.
Esta conjetura ha sido investigada por muchos teóricos de números y ha sido comprobada por ordenadores para todos los números pares menores que 1018. La mayor parte de los matemáticos cree que la conjetura es cierta, y se basan mayoritariamente en las consideraciones estadísticas sobre la distribución probabilística de los números primos en el conjunto de los números naturales: cuanto mayor sea el número entero par, se hace más "probable" que pueda ser escrito como suma de dos números primos.
Enlace.
jueves, 19 de enero de 2012
Paginas de interes
La Cryptogr@phie expliquée!
Aqui hay un applet sobre la maquina enigma muy bien explicado
http://www.bibmath.net/crypto/debvingt/enigmafonc.php3
http://www.bibmath.net/crypto/debvingt/enigmasimul.php3
Aqui hay un applet sobre la maquina enigma muy bien explicado
http://www.bibmath.net/crypto/debvingt/enigmafonc.php3
http://www.bibmath.net/crypto/debvingt/enigmasimul.php3
martes, 10 de enero de 2012
La Piedra Rosetta
La piedra de Rosetta es parte de una antigua estela egipcia de granodiorita con texto grabado que proveyó la clave para el entendimiento moderno de los jeroglíficos egipcios. La inscripción registra un decreto que fue expedido en Menfis en el año 196 antes de Cristo, en favor del rey Ptolomeo V. En el decreto aparecen tres textos: el superior consta de 14 renglones escritos en antiguos jeroglíficos egipcios, el texto medio consta de 32 renglones en egipcio demótico y el texto inferior consta de 53 renglones en griego antiguo
Historia
Se trata del hallazgo casual de una de las más importantes piezas arqueológicas de la historia de la lengua egipcia y, por extensión, de las lenguas antiguas. Fue descubierta el 15 de julio de 1799 por el capitán francés Pierre-François Bouchard en el pueblo egipcio del delta del Nilo denominado Rosetta (también llamado Rashid), cuando las tropas capitaneadas por Napoleón Bonaparte se encontraban construyendo un fuerte, como parte de las actividades militares en la lucha contra las de Gran Bretaña en las tierras de Egipto.
Traduccion
Bajo el reinado del joven, que recibió la soberanía de su padre, señor de las insignias reales, cubierto de gloria, el instaurador del orden en Egipto, piadoso hacia los dioses, superior a sus enemigos, que ha restablecido la vida de los hombres, Señor de la Fiesta de los Treinta Años, igual que Hefaistos el Grande, un rey como el Sol, gran rey sobre el Alto y el Bajo País, descendiente de los dioses Filopáteres, a quien Hefaistos ha dado aprobación, a quien el Sol le ha dado la victoria, la imagen viva de Zeus, hijo del Sol, Ptolomeo, viviendo por siempre, amado de Ptah. En el año noveno, cuando Aetos, hijo de Aetos, era sacerdote de Alejandro y de los dioses Soteres, de los dioses Adelfas, y de los dioses Evergetes, y de los dioses Filopáteres, y del dios Epífanes Eucharistos, siendo Pyrrha, hija de Filinos, athlófora de Berenice Evergetes; siendo Aria, hija de Diógenes, canéfora de Arsínoe Filadelfo; siendo Irene, hija de Ptolomeo, sacerdotisa de Arsínoe Filopátor, en el (día) cuarto del mes Xandikos (o el 18 de Mejir de los egipcios)
Historia, Traduccion
Suscribirse a:
Entradas (Atom)